The emergence of new hotel markets in resort, urban and suburban locations in Indonesia in recent years, has necessitated the need to better understand the economic drivers of these markets. A better understanding has enabled us to build more robust econometric models for hotel feasibility and hotel performance purposes.
We have recently used statistical clustering algorithms to classify 35 Indonesian hotel markets into homogeneous groups so that we could provide an economic rationalization behind the groupings. Using discriminant analysis, each cluster was linked to various economic characteristics such as employment growth, income levels, regional GDP and international tourists. The analysis can be used to improve hotel portfolio diversification strategies for both hotel investment companies and direct-side equity investors.
The advantage of a statistical clustering approach stems from the ability to group markets based on maximizing each group’s within-group homogeneity while also maximizing differences between groups. A more detailed explanation of the clustering technique used is found in the footnote below.
To provide a simple illustration of the clustering technique we have applied our algorithm to annual room occupancies across 33 Indonesian provinces for the period 2006 to 2018 as listed in the table below. Four distinct clusters were identified through the procedure and are shown in the graph below. Additional clusters were not found to produce a significant reduction in total within-cluster variance.
Cluster 1 consists of the largest hotel markets in the country, Bali and Jakarta, as well as other emerging tourist destinations. It accounts for almost 112,000 or 40% of all star rated hotel rooms in Indonesia. The average occupancy for cluster 1 markets rose 7.5 percentage points from 50.4% in 2006 to 57.9% in 2018 as illustrated in graph 2.
Graph 1: The Location of the Four Hotel Market Clusters for Star-Rated Hotels in Indonesia’s Provinces 2006-2018
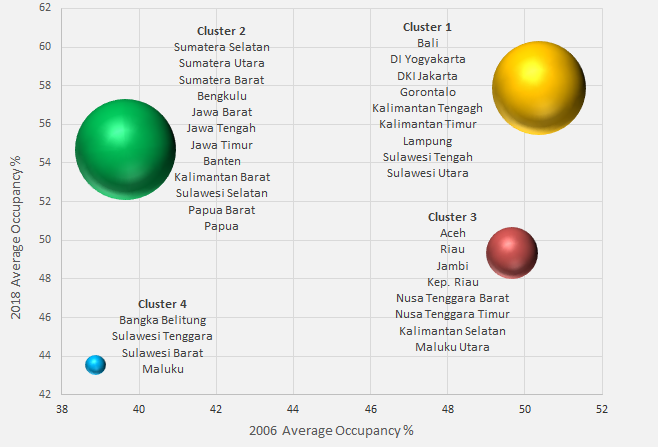
Cluster 2 provinces witnessed the fastest growing occupancy rates over the past 12 years. The average occupancy for Cluster 2 provinces grew from 39.7% in 2006 to 54.7% in 2018, a jump of 15.1 percentage points. Cluster 2 accounts for almost 129,000 rooms or 46% of all star rated hotel rooms.
Cluster 3 provinces, which include the popular tourist destinations of Nusa Tenggara Barat and Maluku Utara, have witnessed flat occupancies throughout the period which have oscillated between 45 and 50%. Cluster 4 provinces, which includes the provinces of Maluku and Sulawesi Tenggara, experienced significant growth in occupancies between 2007 and 2011 and a lack-luster performance since 2011 as illustrated below.
Graph 2: Growth in Average Occupancies for the Four Clusters 2006-2018

The analysis above provides a comparatively simple example of the clustering technique. In our larger assignment on 35 hotel markets throughout the country, we formalized in a statistical sense, the relationship between cluster assignments and the underlying municipal and regency area economic characteristics. Through multiple discriminant analysis (MDA), a linear model was constructed to explain to what degree the cluster membership was related to cross-sectional market demand and economic characteristics.
Our analysis has helped us build more robust models of hotel markets in Indonesia for forecasting hotel metrics such as room demand, occupancy and hotel property returns.
Growth in Room Occupancies for Star-Rated Hotels in Indonesia’s Provinces 2006-2018

K-means clustering
Clustering is the classification of objects or in our case hotel markets into different groups, or more precisely, the partitioning of a data set into subsets (clusters), so that the data in each subset (ideally) share some common trait – often proximity according to some defined distance measure. Data clustering is a common technique for statistical data analysis which is used in many fields, including real estate as illustrated by the references provided below.
The objective of cluster analysis is to assign observations to groups (“clusters”) so that observations within each group are similar to one another with respect to variables or attributes of interest, and the groups themselves stand apart from one another. In other words, the objective is to divide the observations into homogeneous and distinct groups.
The K-means algorithm assigns each point to the cluster whose center (also called centroid) is nearest. The center is the average of all the points in the cluster — that is, its coordinates are the arithmetic mean for each dimension separately over all the points in the cluster.
Example: The data set has three dimensions and the cluster has two points: X = (x1, x2, x3) and Y = (y1, y2, y3). Then the centroid Z becomes Z = (z1, z2, z3), where z1 = (x1 + y1)/2 and z2 = (x2 + y2)/2 and z3 = (x3 + y3)/2.
The algorithm steps are:(1)
• Choose the number of clusters, k.
• Randomly generate k clusters and determine the cluster centers, or directly generate k random points as cluster centers.
• Assign each point to the nearest cluster center.
• Re-compute the new cluster centers.
Repeat the two previous steps until some convergence criterion is me(usually that the assignment hasn’t changed). The main advantages of this algorithm are its simplicity and speed which allows it to run on large datasets. Cluster analysis is often accompanied by discriminant analysis, a statistical analysis tool that identifies the variables that distinguish one cluster from another. This statistical tool involves a linear combination, or variate, of two or more independent (or explanatory) variables that best discriminate between the cluster groups already identified.
(1) MacQueen, J. B. (1967). Some Methods for Classification and Analysis of Multivariate Observations, Proceedings of 5th Berkeley Symposium on Mathematical Statistics and Probability, Berkeley, University of California Press, 1:281-297
Further articles on the application of cluster analysis in real estate include:
(1) Jackson, Cath and White, Michael. Challenging Traditional Real Estate Market Classifications for Investment Diversification. Journal of Real Estate Portfolio Management, Sep-Dec 2005, Vol. 11 Issue 3.
(2) Smith, Allen; Hess, Robert and Youguo Liang. Clustering the U.S. Real Estate Markets. Journal of Real Estate Portfolio Management, May-Aug 2005, Vol. 11 Issue 2.
(3) Cheng, Ping and Black, Roy T. Geographic Diversification and Economic Fundamentals in Apartment Markets: A Demand Perspective. Journal of Real Estate Portfolio Management, 1998, Vol. 4 Issue 2.
(4) Gallagher, Mark and Mansour, Asieh. An Analysis of Hotel Real Estate Market Dynamics. Journal of Real Estate Research, 2000, Vol. 19. No.1/2.
(5) Goetzman, William N. and Wachter, Susan M. Clustering Methods for Real Estate Portfolios. Real Estate Economics, 1995, Vol. 23, Issue 3.
(6) Hunter, Maura Quinn. How to Identify and Evaluate Industry Risk in a Loan Portfolio: A Five Step Approach. The Journal of Lending & Credit Risk Management, 1998, 28-35.